| Home |
|---|
| Outlook |
| Errata |
| Sage codes |
| Bibliography |
| Links |
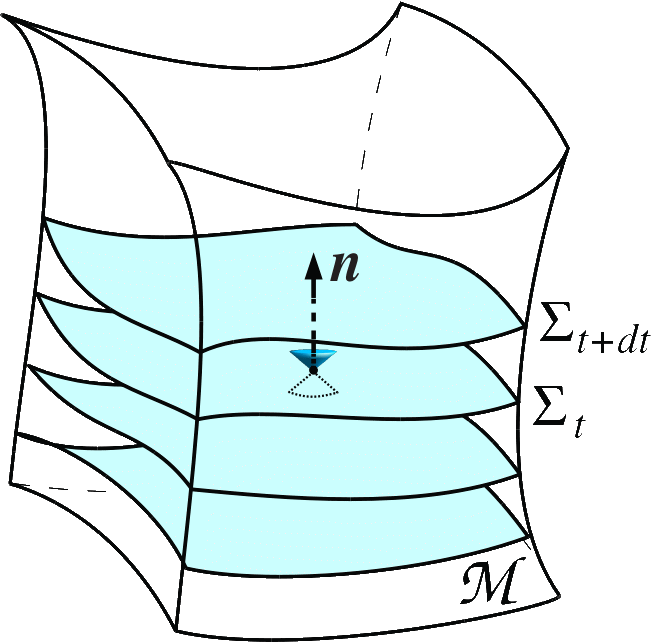 |
[1] https://www.luth.obspm.fr/IHP06/
[2] https://www.smf.mx/~dgfm-smf/EscuelaVII/
[3] https://apctp.org/conferences/
[4] Spectral Einstein Code : https://www.black-holes.org/SpEC.html
[5] Whisky code : https://www.whiskycode.org/
[6] A.M. Abrahams, G.B. Cook, S.L. Shapiro, and S.A. Teukolsky : Solving Einstein’s equations for rotating spacetimes: Evolution of relativistic star clusters, Phys. Rev. D 49, 5153 (1994).
[7] M. Alcubierre : Appearance of coordinate shocks in hyperbolic formalisms of general relativity, Phys. Rev. D 55, 5981 (1997).
[8] M. Alcubierre : The status of numerical relativity, in General Relativity And Gravitation: Proceedings of the 17th International Conference, Dublin, 18-23 July 2004, edited by P. Florides, B. Nolan and A. Ottewill, World Scientific (2005).
[9] M. Alcubierre : Introduction to 3+1 Numerical Relativity, Oxford Univ. Press, Oxford (2008).
[10] M. Alcubierre, W. Benger, B. Brügmann, G. Lanfermann, L. Nerger, E. Seidel, and R. Takahashi : 3D Grazing Collision of Two Black Holes, Phys. Rev. Lett. 87, 271103 (2001).
[11] M. Alcubierre and B. Brügmann : Simple excision of a black hole in 3+1 numerical relativity, Phys. Rev. D 63, 104006 (2001).
[12] M. Alcubierre, B. Brügmann, P. Diener, F. S. Guzmán, I. Hawke, S. Hawley, F. Herrmann, M. Koppitz, D. Pollney, E. Seidel, and J. Thornburg : Dynamical evolution of quasicircular binary black hole data, Phys. Rev. D 72, 044004 (2005).
[13] M. Alcubierre, B. Brügmann, P. Diener, M. Koppitz, D. Pollney, E. Seidel, and R. Takahashi : Gauge conditions for long-term numerical black hole evolutions without excision, Phys. Rev. D 67, 084023 (2003).
[14] M. Alcubierre, B. Brügmann, D. Pollney, E. Seidel, and R. Takahashi : Black hole excision for dynamic black holes, Phys. Rev. D 64, 061501 (2001).
[15] M. Alcubierre, A. Corichi, J.A. González, D. Núñez, B. Reimann, and M. Salgado : Generalized harmonic spatial coordinates and hyperbolic shift conditions, Phys. Rev. D 72, 124018 (2005).
[16] M. Alcubierre, J.C. Degollado, and M. Salgado : Einstein-Maxwell system in 3+1 form and initial data for multiple charged black holes, Phys. Rev. D 80, 104022 (2009)
[17] D. Alic, L. Rezzolla, I. Hinder, & P. Mösta : Dynamical damping terms for symmetry-seeking shift conditions, Class. Quantum Grav. 27, 245023 (2010).
[18] A. Anderson and J.W. York : Hamiltonian Time Evolution for General Relativity, Phys. Rev. Lett. 81, 1154 (1998).
[19] A. Anderson and J.W. York : Fixing Einstein’s Equations, Phys. Rev. Lett. 82, 4384 (1999).
[20] M. Anderson and R.A. Matzner : Extended Lifetime in Computational Evolution of Isolated Black Holes, Found. Phys. 35, 1477 (2005).
[21] L. Andersson : The Global Existence Problem in General Relativity, in Ref. [115], p. 71.
[22] L. Andersson and V. Moncrief : Elliptic-Hyperbolic Systems and the Einstein Equations, Ann. Henri Poincaré 4, 1 (2003).
[23] P. Anninos, J. Massó, E. Seidel, W.-M. Suen, and J. Towns : Three-dimensional numerical relativity: The evolution of black holes, Phys. Rev. D 52, 2059 (1995).
[24] M. Ansorg : Double-domain spectral method for black hole excision data, Phys. Rev. D 72, 024018 (2005).
[25] M. Ansorg: Multi-Domain Spectral Method for Initial Data of Arbitrary Binaries in General Relativity, Class. Quantum Grav. 24, S1 (2007).
[26] M. Ansorg, B. Brügmann and W. Tichy : Single-domain spectral method for black hole puncture data, Phys. Rev. D 70, 064011 (2004).
[27] M. Ansorg and D. Petroff : Negative Komar mass of single objects in regular, asymptotically flat spacetimes, Class. Quantum Grav. 23, L81 (2006).
[28] L. Antón , O. Zanotti, J.A. Miralles, J.M. Martí, J.M. Ibáñez, J.A. Font, and J.A. Pons : Numerical 3+1 General Relativistic Magnetohydrodynamics: A Local Characteristic Approach, Astrophys. J. 637, 296 (2006).
[29] R. Arnowitt, S. Deser and C.W Misner : The Dynamics of General Relativity, in Gravitation: an introduction to current research, edited by L. Witten, Wiley, New York (1962), p. 227; available at https://arxiv.org/abs/gr-qc/0405109.
[30] A. Ashtekar : Asymptotic Structure of the Gravitational Field at Spatial Infinity, in General Relativity and Gravitation, one hundred Years after the Birth of Albert Einstein, Vol. 2, edited by A. Held, Plenum Press, New York (1980), p. 37.
[31] A. Ashtekar and R. O. Hansen : A unified treatment of null and spatial infinity in general relativity. I. Universal structure, asymptotic symmetries, and conserved quantities at spatial infinity, J. Math. Phys. 19, 1542 (1978).
[32] A. Ashtekar and A. Magnon-Ashtekar : On conserved quantities in general relativity, J. Math. Phys. 20, 793 (1979).
[33] R.F. Baierlein, D.H Sharp and J.A. Wheeler : Three-Dimensional Geometry as Carrier of Information about Time, Phys. Rev. 126, 1864 (1962).
[34] L. Baiotti, B. Giacomazzo, and L. Rezzolla : Accurate evolutions of inspiralling neutron-star binaries: Prompt and delayed collapse to a black hole, Phys. Rev. D 78, 084033 (2008).
[35] L. Baiotti, I. Hawke, P.J. Montero, F. Löffler, L. Rezzolla, N. Stergioulas, J.A. Font, and E. Seidel : Three-dimensional relativistic simulations of rotating neutron-star collapse to a Kerr black hole, Phys. Rev. D 71, 024035 (2005).
[36] L. Baiotti, I. Hawke, P.J. Montero, and L. Rezzolla : A new three-dimensional general-relativistic hydrodynamics code, Mem. S.A.It. Suppl. 1, 210 (2003).
[37] L. Baiotti, I. Hawke, L. Rezzolla, and E. Schnetter : Gravitational-Wave Emission from Rotating Gravitational Collapse in Three Dimensions, Phys. Rev. Lett. 94, 131101 (2005).
[38] L. Baiotti and L. Rezzolla : Challenging the Paradigm of Singularity Excision in Gravitational Collapse, Phys. Rev. Lett. 97, 141101 (2006).
[39] L. Baiotti, S. Shibata, and T. Yamamoto : Binary neutron-star mergers with Whisky and SACRA: First quantitative comparison of results from independent general-relativistic hydrodynamics codes, Phys. Rev. D 82, 064015 (2010).
[40] J.G. Baker, M. Campanelli, C.O. Lousto and R. Takahashi : Modeling gravitational radiation from coalescing binary black holes, Phys. Rev. D 65, 124012 (2002).
[41] J.G. Baker, J. Centrella, D.-I. Choi, M. Koppitz, and J. van Meter : Gravitational-Wave Extraction from an Inspiraling Configuration of Merging Black Holes, Phys. Rev. Lett. 96, 111102 (2006).
[42] J.G. Baker, J. Centrella, D.-I. Choi, M. Koppitz, and J. van Meter : Binary black hole merger dynamics and waveforms, Phys. Rev. D 73, 104002 (2006).
[43] F. Banyuls, J. A. Font, J. M. Ibáñez, J. M. Martí, and J. A. Miralles : Numerical 3+1 General Relativistic Hydrodynamics: A Local Characteristic Approach, Astrophys. J. 476, 221 (1997).
[44] J.M. Bardeen : A Variational Principle for Rotating Stars in General Relativity, Astrophys. J. 162, 71 (1970).
[45] J.M. Bardeen : Gauge and radiation conditions in numerical relativity, in Rayonnement gravitationnel / Gravitation Radiation, edited by N. Deruelle and T. Piran, North Holland, Amsterdam (1983), p. 433.
[46] J.M. Bardeen and T. Piran : General relativistic axisymmetric rotating systems: coordinates and equations, Phys. Rep. 96, 206 (1983).
[47] R. Bartnik : Quasi-spherical metrics and prescribed scalar curvature, J. Diff. Geom. 37, 31 (1993).
[48] R. Bartnik and G. Fodor : On the restricted validity of the thin sandwich conjecture, Phys. Rev. D 48, 3596 (1993).
[49] R. Bartnik and J. Isenberg : The Constraint Equations, in Ref. [115], p. 1.
[50] T.W. Baumgarte : Innermost stable circular orbit of binary black holes, Phys. Rev. D 62, 024018 (2000).
[51] T.W. Baumgarte, G.B. Cook, M.A. Scheel, S.L. Shapiro, and S.A. Teukolsky : Binary neutron stars in general relativity: Quasiequilibrium models, Phys. Rev. Lett. 79, 1182 (1997).
[52] T.W. Baumgarte, G.B. Cook, M.A. Scheel, S.L. Shapiro, and S.A. Teukolsky : General relativistic models of binary neutron stars in quasiequilibrium, Phys. Rev. D 57, 7299 (1998).
[53] T.W. Baumgarte and S.G. Naculich : Analytical representation of a black hole puncture solution, Phys. Rev. D 75, 067502 (2007).
[54] T.W. Baumgarte, N. Ó Murchadha, and H.P. Pfeiffer : Einstein constraints: Uniqueness and non-uniqueness in the conformal thin sandwich approach, Phys. Rev. D 75, 044009 (2007).
[55] T.W. Baumgarte and S.L. Shapiro : Numerical integration of Einstein’s field equations, Phys. Rev. D 59, 024007 (1999).
[56] T.W. Baumgarte and S.L. Shapiro : Numerical relativity and compact binaries, Phys. Rep. 376, 41 (2003).
[57] T.W. Baumgarte and S.L. Shapiro : General relativistic magnetohydrodynamics for the numerical construction of dynamical spacetimes, Astrophys. J. 585, 921 (2003).
[58] T. W. Baumgarte and S. L. Shapiro : Numerical Relativity. Solving Einstein’s Equations on the Computer, Cambridge Univ. Press, Cambridge (2010).
[59] R. Beig : Arnowitt-Deser-Misner energy and g00, Phys. Lett. 69A, 153 (1978).
[60] R. Beig : The maximal slicing of a Schwarzschild black hole, Ann. Phys. (Leipzig) 11, 507 (2000).
[61] R. Beig and W. Krammer : Bowen-York tensors, Class. Quantum Grav. 21, S73 (2004).
[62] R. Beig and N. Ó Murchadha : Late time behavior of the maximal slicing a the Schwarzschild black hole, Phys. Rev. D 57, 4728 (1998).
[63] M. Bejger, D. Gondek-Rosińska, E. Gourgoulhon, P. Haensel, K. Taniguchi, and J. L. Zdunik : Impact of the nuclear equation of state on the last orbits of binary neutron stars, Astron. Astrophys. 431, 297-306 (2005).
[64] M. Berger : A Panoramic View of Riemannian Geometry, Springer, Berlin (2003).
[65] M. Berger and B. Gostiaux : Géométrie différentielle: variétés, courbes et surfaces, Presses Universitaires de France, Paris (1987).
[66] D. H. Bernstein : A Numerical Study of the Black Hole Plus Brill Wave Spacetime, PhD Thesis, Dept. of Physics, University of Illinois at Urbana-Champaign (1993).
[67] H. Beyer and O. Sarbach : Well-posedness of the Baumgarte-Shapiro-Shibata-Nakamura formulation of Einstein’s field equations, Phys. Rev. D 70, 104004 (2004).
[68] L. Blanchet : Innermost circular orbit of binary black holes at the third post-Newtonian approximation, Phys. Rev. D 65, 124009 (2002).
[69] L. Blanchet : Gravitational Radiation from Post-Newtonian Sources
and Inspiralling Compact Binaries, Living Rev. Relativity 9, 4 (2006);
https://www.livingreviews.org/lrr-2006-4
[70] L. Blanchet : Theory of Gravitational Wave Emission, lectures at Institut Henri Poincaré, Paris (2006); available at https://www.luth.obspm.fr/IHP06/
[71] C. Bona, L. Lehner, and C. Palenzuela-Luque : Geometrically motivated hyperbolic coordinate conditions for numerical relativity: Analysis, issues and implementations, Phys. Rev. D 72, 104009 (2005).
[72] C. Bona and J. Massó : Harmonic synchronizations of spacetime, Phys. Rev. D 38, 2419 (1988).
[73] C. Bona, J. Massó, E. Seidel, and J. Stela : New Formalism for Numerical Relativity, Phys. Rev. Lett. 75, 600 (1995).
[74] C. Bona, J. Massó, E. Seidel, and J. Stela : First order hyperbolic formalism for numerical relativity, Phys. Rev. D 56, 3405 (1997).
[75] C. Bona, C. Palenzuela-Luque, and C. Bona-Casas : Elements of Numerical Relativity and Relativistic Hydrodynamics: From Einstein’s Equations to Astrophysical Simulations (2nd edition), Springer, Berlin (2009).
[76] S. Bonazzola, E. Gourgoulhon, P. Grandclément, and J. Novak : Constrained scheme for the Einstein equations based on the Dirac gauge and spherical coordinates, Phys. Rev. D 70, 104007 (2004).
[77] S. Bonazzola, E. Gourgoulhon, and J.-A. Marck : Numerical models of irrotational binary neutron stars in general relativity, Phys. Rev. Lett. 82, 892 (1999).
[78] J.M. Bowen and J.W. York : Time-asymmetric initial data for black holes and black-hole collisions, Phys. Rev. D 21, 2047 (1980).
[79] S. Brandt and B. Brügmann : A Simple Construction of Initial Data for Multiple Black Holes, Phys. Rev. Lett. 78, 3606 (1997).
[80] S.R. Brandt and E. Seidel : Evolution of distorted rotating black holes. II. Dynamics and analysis, Phys. Rev. D 52, 870 (1995).
[81] J.D. Brown : Probing the puncture for black hole simulations, Phys. Rev. D 80, 084042 (2009).
[82] B. Brügmann : Binary Black Hole Mergers in 3d Numerical Relativity, Int. J. Mod. Phys. D 8, 85 (1999).
[83] B. Brügmann, J.A. González, M. Hannam, S. Husa, U. Sperhake, and W. Tichy : Calibration of moving puncture simulations, Phys. Rev. D 77, 024027 (2008).
[84] B. Brügmann, W. Tichy and N. Jansen : Numerical Simulation of Orbiting Black Holes, Phys. Rev. Lett. 92, 211101 (2004).
[85] N. Bucciantini and L. Del Zanna : General relativistic magnetohydrodynamics in axisymmetric dynamical spacetimes: the X-ECHO code, Astron. Astrophys. 528, A101 (2011).
[86] A. Buonanno : Binary Black Hole Coalescence, in Astrophysics of Compact Objects, edited by Y.-F. Yuan, X.-D. Li and D. Lai, AIP Conference Proceedings 968, 307 (2008).
[87] A. Buonanno, G.B. Cook, and F. Pretorius : Inspiral, merger, and ring-down of equal-mass black-hole binaries, Phys. Rev. D 75, 124018 (2007).
[88] A. Buonanno and T. Damour : Effective one-body approach to general relativistic two-body dynamics, Phys. Rev. D 59, 084006 (1999).
[89] A. Buonanno, L.E. Kidder, A.H. Mroué, H.P. Pfeiffer, and A. Taracchini : Reducing orbital eccentricity of precessing black-hole binaries, Phys. Rev. D 83, 104034 (2011).
[90] A. Čadež : Some remarks on the two-body-problem in geometrodynamics, Ann. Phys. (N.Y.) 91, 58 (1975).
[91] M. Campanelli, C. O. Lousto, P. Marronetti, and Y. Zlochower : Accurate Evolutions of Orbiting Black-Hole Binaries without Excision, Phys. Rev. Lett. 96, 111101 (2006).
[92] M. Campanelli, C. O. Lousto, and Y. Zlochower : Last orbit of binary black holes, Phys. Rev. D 73, 061501(R) (2006).
[93] M. Campanelli, C. O. Lousto, and Y. Zlochower : Spinning-black-hole binaries: The orbital hang-up, Phys. Rev. D 74, 041501(R) (2006).
[94] M. Campanelli, C. O. Lousto, and Y. Zlochower : Spin-orbit interactions in black-hole binaries, Phys. Rev. D 74, 084023 (2006).
[95] M. Cantor: The existence of non-trivial asymptotically flat initial data for vacuum spacetimes, Commun. Math. Phys. 57, 83 (1977).
[96] M. Cantor : Some problems of global analysis on asymptotically
simple manifolds, Compositio Mathematica 38, 3 (1979);
available at https://www.numdam.org/item?id=CM_1979__38_1_3_0
[97] S.M. Carroll : Spacetime and Geometry: An Introduction to General
Relativity, Addison Wesley (Pearson Education), San Fransisco (2004);
https://preposterousuniverse.com/spacetimeandgeometry/
[98] B. Carter : Outer curvature and conformal geometry of an imbedding, J. Geom. Phys. 8, 53 (1992).
[99] B. Carter : Basic brane theory, Class. Quantum Grav. 9, S19 (1992).
[100] B. Carter : Extended tensorial curvature analysis for embeddings and foliations, Contemp. Math. 203, 207 (1997).
[101] M. Caudill, G.B. Cook, J.D. Grigsby, and H.P. Pfeiffer : Circular orbits and spin in black-hole initial data, Phys. Rev. D 74, 064011 (2006).
[102] J. M. Centrella, J. G. Baker, B. J. Kelly, and J. R. van Meter : Black-hole binaries, gravitational waves, and numerical relativity, Rev. Mod. Phys. 82, 3069 (2010).
[103] P. Cerdá-Durán, J. A. Font, L. Antón, and E. Müller : A new general relativistic magnetohydrodynamics code for dynamical spacetimes, Astron. Astrophys. 492, 937 (2008).
[104] M.W. Choptuik : Numerical Analysis for Numerical Relativists,
lecture at the VII Mexican School on Gravitation and Mathematical
Physics, Playa del Carmen (Mexico), 26 November - 1 December 2006
[2];
available at https://laplace.physics.ubc.ca/People/matt/Teaching/06Mexico/
[105] M.W. Choptuik, E.W. Hirschmann, S.L. Liebling, and F. Pretorius : An axisymmetric gravitational collapse code, Class. Quantum Grav. 20, 1857 (2003).
[106] Y. Choquet-Bruhat : New elliptic system and global solutions for the constraints equations in general relativity, Commun. Math. Phys. 21, 211 (1971).
[107] Y. Choquet-Bruhat : General Relativity and Einstein’s Equations, Oxford Univ. Press, New York (2009).
[108] Y. Choquet-Bruhat, C. De Witt-Moretten, and M. Dillard-Bleick : Analysis, Manifolds and Physics, North-Holland, Amsterdam (1977).
[109] Y. Choquet-Bruhat and R. Geroch : Global Aspects of the Cauchy Problem in General Relativity, Commun. Math. Phys. 14, 329 (1969).
[110] Y. Choquet-Bruhat and J.W. York : The Cauchy Problem, in General Relativity and Gravitation, one hundred Years after the Birth of Albert Einstein, Vol. 1, edited by A. Held, Plenum Press, New York (1980), p. 99.
[111] Y. Choquet-Bruhat and D. Christodoulou : Elliptic systems of Hs,δ spaces on manifolds which are Euclidean at infinity, Acta Math. 146, 129 (1981)
[112] Y. Choquet-Bruhat and T. Ruggeri : Hyperbolicity of the 3+1 system of Einstein equations, Commun. Math. Phys. 89, 269 (1983).
[113] Y. Choquet-Bruhat, J. Isenberg, and J.W. York : Einstein constraints on asymptotically Euclidean manifolds, Phys. Rev. D 61, 084034 (2000).
[114] P.T. Chruściel : On angular momentum at spatial infinity, Class. Quantum Grav. 4, L205 (1987).
[115] P.T. Chruściel and H. Friedrich (Eds.), The Einstein Equations and the Large Scale Behavior of Gravitational Fields — 50 years of the Cauchy Problem in General Relativity, Birkhäuser Verlag, Basel (2004).
[116] P.T. Chruściel, G.J. Galloway, and D. Pollack : Mathematical general relativity: A sampler, Bull. Amer. Math. Soc. 47, 567 (2010).
[117] G.B. Cook : Initial data for numerical relativity, Living Rev. Relativity 3, 5 (2000); https://www.livingreviews.org/lrr-2000-5
[118] G.B. Cook and H.P. Pfeiffer : Excision boundary conditions for black-hole initial data, Phys. Rev. D 70, 104016 (2004).
[119] G.B. Cook and M.A. Scheel : Well-Behaved Harmonic Time Slices of a Charged, Rotating, Boosted Black Hole, Phys. Rev. D 56, 4775 (1997).
[120] G.B. Cook, S.L. Shapiro and S.A. Teukolsky : Testing a simplified version of Einstein’s equations for numerical relativity, Phys. Rev. D 53, 5533 (1996).
[121] I. Cordero-Carrión, P. Cerdá-Durán, H. Dimmelmeier, J.L. Jaramillo, J. Novak and E. Gourgoulhon : Improved constrained scheme for the Einstein equations: An approach to the uniqueness issue, Phys. Rev. D 79, 024017 (2009).
[122] I. Cordero-Carrión, P. Cerdá-Durán, and J.M. Ibáñez : Dynamical spacetimes and gravitational radiation in a Fully Constrained Formulation, J. Phys.: Conf. Ser. 228, 012055 (2010).
[123] I. Cordero-Carrión, P. Cerdá-Durán, and J.M. Ibáñez : Gravitational waves in dynamical spacetimes with matter content in the Fully Constrained Formulation, preprint arXiv:1108.0571.
[124] I. Cordero-Carrión, J.M. Ibáñez, E. Gourgoulhon, J.L. Jaramillo and J. Novak : Mathematical Issues in a Fully-Constrained Formulation of Einstein Equations, Phys. Rev. D 77, 084007 (2008).
[125] I. Cordero-Carrión, J.M. Ibáñez, J.A. Morales-Lladosa : Maximal slicings in spherical symmetry: Local existence and construction, J. Math. Phys. 52, 112501 (2011).
[126] J. Corvino : Scalar curvature deformation and a gluing construction for the Einstein constraint equations, Commun. Math. Phys. 214, 137 (2000).
[127] E. Cotton : Sur les variétés à trois dimensions, Annales de la faculté
des sciences de Toulouse Sér. 2, 1, 385 (1899);
available at
https://www.numdam.org/item?id=AFST_1899_2_1_4_385_0
[128] R. Courant and D. Hilbert : Methods of Mathematical Physics; vol. II : Partial Differential Equations, Interscience, New York (1962).
[129] M. Dahl, R. Gicquaud, and E. Humbert : A limit equation associated to the solvability of the vacuum Einstein constraint equations using the conformal method, preprint arXiv:1012.2188.
[130] S. Dain : Trapped surfaces as boundaries for the constraint equations, Class. Quantum Grav. 21, 555 (2004); errata in Class. Quantum Grav. 22, 769 (2005).
[131] S. Dain : Elliptic systems, in Analytical and Numerical Approaches to Mathematical Relativity, edited by J. Frauendiener, D.J.W. Giulini, and V. Perlick, Lect. Notes Phys. 692, Springer, Berlin (2006), p. 117.
[132] S. Dain, J.L. Jaramillo, and B. Krishnan : On the existence of initial data containing isolated black holes, Phys.Rev. D 71, 064003 (2005).
[133] T. Damour : Coalescence of two spinning black holes: An effective one-body approach, Phys. Rev. D 64, 124013 (2001).
[134] T. Damour : Advanced General Relativity, lectures at Institut Henri Poincaré, Paris (2006), available at https://www.luth.obspm.fr/IHP06/
[135] T. Damour, E. Gourgoulhon, and P. Grandclément : Circular orbits of corotating binary black holes: comparison between analytical and numerical results, Phys. Rev. D 66, 024007 (2002).
[136] T. Damour and A. Nagar : Effective one body description of tidal effects in inspiralling compact binaries, Phys. Rev. D 81, 084016 (2010).
[137] G. Darmois : Les équations de la gravitation einsteinienne,
Mémorial des Sciences Mathématiques 25, Gauthier-Villars, Paris
(1927);
available at https://www.numdam.org/item?id=MSM_1927__25__1_0
[138] T. De Donder : La Gravifique einsteinienne, Gauthier-Villars, Paris (1921); see Ref. [139] for a related freely downloadable version.
[139] T. De Donder : La Gravifique Einsteinienne, Ann. Inst. H. Poincaré 1, 77 (1930); available at https://www.numdam.org/item?id=AIHP_1930__1_2_77_0
[140] N. Deruelle : General Relativity: a Primer, lectures at Institut Henri Poincaré, Paris (2006), available at https://www.luth.obspm.fr/IHP06/
[141] S. Deser : Some Remarks on Dirac’s Contributions to General Relativity, Int. J. Mod. Phys. A 19S1, 99 (2004).
[142] S. Detweiler : Periodic solutions of the Einstein equations for binary systems, Phys. Rev. D 50, 4929 (1994).
[143] P. Diener, F. Herrmann, D. Pollney, E. Schnetter, E. Seidel, R. Takahashi, J. Thornburg, and J. Ventrella : Accurate Evolution of Orbiting Binary Black Holes, Phys. Rev. Lett. 96, 121101 (2006).
[144] H. Dimmelmeier, J.A. Font, and E. Müller : Relativistic simulations of rotational core collapse I. Methods, initial models, and code tests, Astron. Astrophys. 388, 917 (2002).
[145] H. Dimmelmeier, J.A. Font, and E. Müller : Relativistic simulations of rotational core collapse II. Collapse dynamics and gravitational radiation, Astron. Astrophys. 393, 523 (2002).
[146] H. Dimmelmeier, J. Novak, J.A. Font, J.M. Ibáñez, and E. Müller : Combining spectral and shock-capturing methods: A new numerical approach for 3D relativistic core collapse simulations, Phys. Rev. D 71, 064023 (2005).
[147] P.A.M. Dirac : The Theory of gravitation in Hamiltonian form, Proc. Roy. Soc. Lond. A 246, 333 (1958).
[148] P.A.M. Dirac : Fixation of Coordinates in the Hamiltonian Theory of gravitation, Phys. Rev. 114, 924 (1959).
[149] M.D. Duez : Numerical relativity confronts compact neutron star binaries: a review and status report, Class. Quantum Grav. 27, 114002 (2010).
[150] M.D. Duez, F. Foucart, L.E. Kidder, H.P. Pfeiffer, M.A. Scheel, and S.A. Teukolsky : Evolving black hole-neutron star binaries in general relativity using pseudospectral and finite difference methods, Phys. Rev. D 78, 104015 (2008).
[151] M.D. Duez, Y.T. Liu, S.L. Shapiro, and B.C. Stephens : Relativistic magnetohydrodynamics in dynamical spacetimes: Numerical methods and tests, Phys. Rev. D 72, 024028 (2005).
[152] G.F.R. Ellis and H. van Elst : Cosmological Models, in Theoretical and observational cosmology : proceedings of the NATO Advanced Study Institute on Theoretical and Observational Cosmology, Cargèse, France, August 17-29, 1998, edited by M. Lachièze-Rey., Kluwer Academic, Boston (1999), p. 1.
[153] H. Eschrig : Topology and Geometry for Physics, Springer, Berlin (2011).
[154] F. Estabrook, H. Wahlquist, S. Christensen, B. DeWitt, L. Smarr, and E. Tsiang : Maximally Slicing a Black Hole, Phys. Rev. D 7, 2814 (1973).
[155] Z.B. Etienne, Y.T. Liu, and S.L. Shapiro : Relativistic magnetohydrodynamics in dynamical spacetimes: A new adaptive mesh refinement implementation, Phys. Rev. D 82, 084031 (2010).
[156] C.R. Evans : An approach for calculating axisymmetric gravitational collapse, in Dynamical spacetimes and numerical relativity, edited by J. Centrella, Cambridge Univ. Press, Cambridge (1986), p. 3.
[157] C.R. Evans : Enforcing the momentum constraints during axisymmetric spacelike simulations, in Frontiers in Numerical Relativity, edited by C.R. Evans, L.S. Finn, and D.W. Hobill, Cambridge Univ. Press, Cambridge (1989), p. 194.
[158] J.A. Faber, P. Grandclément, and F.A. Rasio : Mergers of irrotational neutron star binaries in conformally flat gravity, Phys. Rev. D 69, 124036 (2004).
[159] A. E. Fischer and J. Marsden : The Einstein Equation of Evolution – A Geometric Approach, J. Math. Phys. 13, 546 (1972).
[160] A. Fischer and J. Marsden : The initial value problem and the dynamical formulation of general relativity, in General Relativity: an Einstein Centenary Survey, edited by S.W. Hawking and W. Israel, Cambridge Univ. Press, Cambridge (1979), p. 138.
[161] J. A. Font : Numerical Hydrodynamics and Magnetohydrodynamics in General Relativity, Living Rev. Relativity 11, 7 (2008); https://www.livingreviews.org/lrr-2008-7
[162] J. A. Font : An introduction to relativistic hydrodynamics, J. Phys. Conf. Ser. 91, 012002 (2007).
[163] J.A. Font, T. Goodale, S. Iyer, M. Miller, L. Rezzolla, E. Seidel, N. Stergioulas, W.-M. Suen, and M. Tobias : Three-dimensional numerical general relativistic hydrodynamics. II. Long-term dynamics of single relativistic stars, Phys. Rev. D 65, 084024 (2002).
[164] Y. Fourès-Bruhat (Y. Choquet-Bruhat) : Sur l’intégration des équations d’Einstein, C. R. Acad. Sci. Paris 226, 1071 (1948).
[165] Y. Fourès-Bruhat (Y. Choquet-Bruhat) : Théorème d’existence
pour certains systèms d’équations aux dérivées partielles non linéaires,
Acta Mathematica 88, 141 (1952);
available at https://fanfreluche.math.univ-tours.fr/
[166] Y. Fourès-Bruhat (Y. Choquet-Bruhat) : Sur l’Intégration des Équations de la Relativité Générale, J. Rational Mech. Anal. 5, 951 (1956).
[167] J. Frauendiener : Conformal Infinity, Living Rev. Relativity 7, 1
(2004);
https://www.livingreviews.org/lrr-2004-1
[168] J. Frauendiener and H. Friedrich (Eds.) : The conformal structure of space-times: Geometry, Analysis, Numerics, Lecture Notes in Physics 604, Springer-Verlag, Heidelberg (2002).
[169] J.L. Friedman : The Cauchy Problem on Spacetimes That Are Not Globally Hyperbolic, in Ref. [115], p. 331.
[170] J.L. Friedman, K. Uryu and M. Shibata : Thermodynamics of binary black holes and neutron stars, Phys. Rev. D 65, 064035 (2002); erratum in Phys. Rev. D 70, 129904(E) (2004).
[171] H. Friedrich : On the hyperbolicity of Einstein’s and other gauge field equations, Commun. Math. Phys. 100, 525 (1985).
[172] H. Friedrich : Conformal Einstein evolution, in Ref. [168], p. 1.
[173] H. Friedrich and A. Rendall : The Cauchy problem for the Einstein equations, in Einstein’s Field Equations and Their Physical Implications: Selected Essays in Honour of Jürgen Ehlers, edited by B.G. Schmidt, Lecture Notes in Physics 540, Springer, Berlin (2000), p. 127.
[174] S. Frittelli : Note on the propagation of the constraints in standard 3+1 general relativity, Phys. Rev. D 55, 5992 (1997).
[175] S. Frittelli and O.A. Reula : First-Order Symmetric Hyperbolic Einstein Equations with Arbitrary Fixed Gauge, Phys. Rev. Lett. 76, 4667 (1996).
[176] C.F. Gammie, J.C. McKinney, and G. Tóth : HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics, Astrophys. J. 589, 444 (2003).
[177] A. Garat and R.H. Price : Nonexistence of conformally flat slices of the Kerr spacetime, Phys. Rev. D 61, 124011 (2000).
[178] D. Garfinkle : Harmonic coordinate method for simulating generic singularities, Phys. Rev. D 65, 044029 (2002).
[179] R. Geroch : Domain of Dependence, J. Math. Phys. 11, 437 (1970).
[180] B. Giacomazzo and L. Rezzolla : WhiskyMHD: a new numerical code for general relativistic magnetohydrodynamics, Class. Quantum Grav. 24, S235 (2007).
[181] B. Giacomazzo, L. Rezzolla and L. Baioti : Accurate evolutions of inspiralling and magnetized neutron stars: Equal-mass binaries, Phys. Rev. D 83, 044014 (2011).
[182] G.W. Gibbons and J.M. Stewart : Absence of asymptotically flat solutions of Einstein’s equations which are periodic and empty near infinity, in Classical General Relativity, Eds. W.B. Bonnor, J.N. Islam and M.A.H. MacCallum Cambridge Univ. Press, Cambridge (1983), p. 77.
[183] R. Gicquaud and A. Sakovich : A large class of non constant mean curvature solutions of the Einstein constraint equations on an asymptotically hyperbolic manifold, preprint arXiv:1012.2246.
[184] R.J. Gleiser, C.O. Nicasio, R.H. Price, and J. Pullin : Evolving the Bowen-York initial data for spinning black holes, Phys. Rev. D 57, 3401 (1998).
[185] S. K. Godunov : A finite difference method for the numerical computation and discontinuous solutions of the equations of fluid dynamics (in Russian), Math. Sbornik 47, 271 (1959).
[186] E. Gourgoulhon : Simple equations for general relativistic hydrodynamics in spherical symmetry applied to neutron star collapse, Astron Astrophys. 252, 651 (1991).
[187] E. Gourgoulhon : An introduction to relativistic hydrodynamics, in
Stellar Fluid Dynamics and Numerical Simulations: From the Sun to
Neutron Stars, edited by M. Rieutord & B. Dubrulle, EAS Publications
Series 21, EDP Sciences, Les Ulis (2006), p. 43;
available at https://arxiv.org/abs/gr-qc/0603009.
[188] E. Gourgoulhon : Construction of initial data for 3+1 numerical relativity, in Proceedings of the VII Mexican School on Gravitation and Mathematical Physics, held in Playa del Carmen, Mexico (Nov. 26 - Dec. 2, 2006), J. Phys.: Conf. Ser. 91, 012001 (2007).
[189] E. Gourgoulhon : Constrained schemes for evolving the 3+1
Einstein equations, presentation at the CoCoNuT Meeting 2009
(Valencia, Spain, 4-6 November 2009); available at
https://www.mpa-garching.mpg.de/hydro/COCONUT/valencia2009/intro.php
[190] E. Gourgoulhon : Relativité restreinte, des particules à l’astrophysique, EDP Sciences, Les Ulis / CNRS Éditions, Paris (2010).
[191] E. Gourgoulhon, P. Grandclément, and S. Bonazzola : Binary black holes in circular orbits. I. A global spacetime approach, Phys. Rev. D 65, 044020 (2002).
[192] E. Gourgoulhon, P. Grandclément, K. Taniguchi, J.-A. Marck, and S. Bonazzola : Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity: Method and tests, Phys. Rev. D 63, 064029 (2001).
[193] E. Gourgoulhon and J.L. Jaramillo : A 3+1 perspective on null hypersurfaces and isolated horizons, Phys. Rep. 423, 159 (2006).
[194] P. Grandclément : Accurate and realistic initial data for black hole-neutron star binaries, Phys. Rev. D 74, 124002 (2006); erratum in Phys. Rev. D 75, 129903(E) (2007).
[195] P. Grandclément : KADATH: A spectral solver for theoretical physics, J. Comput. Phys. 229, 3334 (2010).
[196] P. Grandclément, S. Bonazzola, E. Gourgoulhon, and J.-A. Marck : A multi-domain spectral method for scalar and vectorial Poisson equations with non-compact sources, J. Comput. Phys. 170, 231 (2001).
[197] P. Grandclément, E. Gourgoulhon, and S. Bonazzola : Binary black holes in circular orbits. II. Numerical methods and first results, Phys. Rev. D 65, 044021 (2002).
[198] P. Grandclément and J. Novak : Spectral methods for numerical
relativity, Living Rev. Relat. 12, 1 (2009);
https://www.livingreviews.org/lrr-2009-1
[199] C. Gundlach, G. Calabrese, I. Hinder, and J.M. Martín-García : Constraint damping in the Z4 formulation and harmonic gauge, Class. Quantum Grav. 22, 3767 (2005).
[200] C. Gundlach and J.M. Martín-García : Well-posedness of formulations of the Einstein equations with dynamical lapse and shift conditions, Phys. Rev. D 74, 024016 (2006).
[201] M.D. Hannam : Quasicircular orbits of conformal thin-sandwich puncture binary black holes, Phys. Rev. D 72, 044025 (2005).
[202] M.D. Hannam, C.R. Evans, G.B Cook and T.W. Baumgarte : Can a combination of the conformal thin-sandwich and puncture methods yield binary black hole solutions in quasiequilibrium?, Phys. Rev. D 68, 064003 (2003).
[203] M. Hannam, S. Husa, F. Ohme, B. Brügmann, and N. Ó Murchadha : Wormholes and trumpets: Schwarzschild spacetime for the moving-puncture generation, Phys. Rev. D 78, 064020 (2008).
[204] J.B. Hartle : Gravity: An Introduction to Einstein’s General
Relativity, Addison Wesley (Pearson Education), San Fransisco (2003);
https://wps.aw.com/aw_hartle_gravity_1/0,6533,512494-,00.html
[205] S.W. Hawking and G.F.R. Ellis : The large scale structure of space-time, Cambridge Univ. Press, Cambridge (1973).
[206] M. Henneaux : Hamiltonian Formalism of General Relativity, lectures at Institut Henri Poincaré, Paris (2006), https://www.luth.obspm.fr/IHP06/
[207] F. Herrmann, I. Hinder, D. Shoemaker, P. Laguna and R.A. Matzner: Gravitational Recoil from Spinning Binary Black Hole Mergers, Astrophys. J. 661, 430 (2007).
[208] F. Herrmann, I. Hinder, D. Shoemaker, and P. Laguna : Unequal mass binary black hole plunges and gravitational recoil, Class. Quantum Grav. 24, S33 (2007).
[209] K. Hotokezaka, K. Kyutoku, H. Okawa, M. Shibata, and K. Kiuchi : Binary neutron star mergers: Dependence on the nuclear equation of state, Phys. Rev. D 83, 124008 (2011).
[210] J.A. Isenberg : Waveless Approximation Theories of Gravity, preprint University of Maryland (1978); published in Int. J. Mod. Phys. D 17, 265 (2008); also available as https://arxiv.org/abs/gr-qc/0702113; an abridged version can be found in Ref. [213].
[211] J. Isenberg : Constant mean curvature solutions of the Einstein constraint equations on closed manifolds, Class. Quantum Grav. 12, 2249 (1995).
[212] J. Isenberg, R. Mazzeo, and D. Pollack : Gluing and wormholes for the Einstein constraint equations, Commun. Math. Phys. 231, 529 (2002).
[213] J. Isenberg and J. Nester : Canonical Gravity, in General Relativity and Gravitation, one hundred Years after the Birth of Albert Einstein, Vol. 1, edited by A. Held, Plenum Press, New York (1980), p. 23.
[214] J. D. Jackson : Classical Electrodynamics (2nd edition), Wiley, New York (1975).
[215] R.T. Jantzen and J.W. York : New Minimal Distortion Shift Gauge, Phys. Rev. D 73, 104008 (2006).
[216] J.L. Jaramillo, M. Ansorg, F. Limousin : Numerical implementation of isolated horizon boundary conditions, Phys. Rev. D 75, 024019 (2007).
[217] J.L. Jaramillo and E. Gourgoulhon : Mass and Angular Momentum in General Relativity, in Mass and Motion in General Relativity, edited by L. Blanchet, A. Spallicci and B. Whiting, Fundamental Theories of Physics 162, 87, Springer, Dordrecht (2011).
[218] J.L. Jaramillo, E. Gourgoulhon, and G.A. Mena Marugán : Inner boundary conditions for black hole initial data derived from isolated horizons, Phys. Rev. D 70, 124036 (2004).
[219] J.L. Jaramillo, J.A. Valiente Kroon, and E. Gourgoulhon : From Geometry to Numerics: interdisciplinary aspects in mathematical and numerical relativity, Class. Quantum Grav. 25, 093001 (2008).
[220] J. Katz : A note on Komar’s anomalous factor, Class. Quantum Grav. 2, 423 (1985).
[221] J. Katz, J. Bi ák and D. Lynden-Bell : Relativistic conservation
laws and integral constraints for large cosmological perturbations, Phys.
Rev. D 55, 5957 (1997).
ák and D. Lynden-Bell : Relativistic conservation
laws and integral constraints for large cosmological perturbations, Phys.
Rev. D 55, 5957 (1997).
[222] L.E. Kidder, L. Lindblom, M.A. Scheel, L.T. Buchman, and H.P. Pfeiffer : Boundary conditions for the Einstein evolution system, Phys. Rev. D 71, 064020 (2005).
[223] L.E. Kidder, M.A. Scheel, and S.A. Teukolsky : Extending the lifetime of 3D black hole computations with a new hyperbolic system of evolution equations, Phys. Rev. D 64, 064017 (2001).
[224] K. Kiuchi, Y. Sekiguchi, M. Shibata, and K. Taniguchi : Long-term general relativistic simulation of binary neutron stars collapsing to a black hole, Phys. Rev. D 80, 064037 (2009).
[225] K. Kiuchi, M. Shibata, and S. Yoshida : Evolution of neutron stars with toroidal magnetic fields: Axisymmetric simulation in full general relativity, Phys. Rev. D 78, 024029 (2008).
[226] K. Kiuchi, S. Yoshida, and M. Shibata : Non-axisymmetric instabilities of neutron star with toroidal magnetic fields, Astron. Astrophys. 532, A30 (2011).
[227] S. Klainerman and F. Nicolò : On the local and global aspects of the Cauchy problem in general relativity, Class. Quantum Grav. 16, R73 (1999).
[228] C. Klein : Binary black hole spacetimes with a helical Killing vector, Phys. Rev. D 70, 124026 (2004).
[229] A.M. Knapp, E.J. Walker, and T.W. Baumgarte : Illustrating stability properties of numerical relativity in electrodynamics, Phys. Rev. D 65, 064031 (2002).
[230] A. Komar : Covariant Conservation Laws in General Relativity, Phys. Rev. 113, 934 (1959).
[231] S.S. Komissarov : Observations of the Blandford-Znajek process and the magnetohydrodynamic Penrose process in computer simulations of black hole magnetospheres, Mon. Not. Roy. Astron. Soc. 359, 801 (2005).
[232] K. Kyutoku, M. Shibata, and K. Taniguchi : Gravitational waves from nonspinning black hole-neutron star binaries: Dependence on equations of state, Phys. Rev. D 82, 044049 (2010).
[233] P. Laguna : Conformal-thin-sandwich initial data for a single boosted or spinning black hole puncture, Phys. Rev. D 69, 104020 (2004).
[234] L. Lehner : Numerical relativity: a review, Class. Quantum Grav. 18, R25 (2001).
[235] L. Lehner and O. Reula : Status Quo and Open Problems in the Numerical Construction of Spacetimes, in Ref. [115], p. 205.
[236] J. Leray : Hyperbolic differential equations, lecture notes, Institute of Advanced Studies, Princeton (1953).
[237] A. Lichnerowicz : Sur certains problèmes globaux relatifs au système
des équations d’Einstein, Hermann, Paris (1939);
available at
https://www.numdam.org/item?id=THESE_1939__226__1_0
[238] A. Lichnerowicz : L’intégration des équations de la gravitation relativiste et le problème des n corps, J. Math. Pures Appl. 23, 37 (1944); reprinted in A. Lichnerowicz : Choix d’œuvres mathématiques, Hermann, Paris (1982), p. 4.
[239] A. Lichnerowicz : Sur les équations relativistes de la gravitation,
Bulletin de la S.M.F. 80, 237 (1952);
available at
https://www.numdam.org/item?id=BSMF_1952__80__237_0
[240] S. L. Liebling, L. Lehner, D. Neilsen, and C. Palenzuela : Evolutions of magnetized and rotating neutron stars, Phys. Rev. D 81, 124023 (2010).
[241] F. Limousin, D. Gondek-Rosińska, and E. Gourgoulhon : Last orbits of binary strange quark stars, Phys. Rev. D 71, 064012 (2005).
[242] L.-M. Lin and J. Novak : Rotating star initial data for a constrained scheme in numerical relativity, Class. Quantum Grav. 23, 4545 (2006).
[243] L. Lindblom and M. A. Scheel : Dynamical gauge conditions for the Einstein evolution equations, Phys. Rev. D 67, 124005 (2003).
[244] L. Lindblom, M. A. Scheel, L. E. Kidder, R. Owen, and O. Rinne : A new generalized harmonic evolution system, Class. Quantum Grav. 23, S447 (2006).
[245] G. Lovelace : Reducing spurious gravitational radiation in binary-black-hole simulations by using conformally curved initial data, Class. Quantum Grav. 26, 114002 (2009).
[246] G. Lovelace, R. Owen, H.P. Pfeiffer, and T. Chu : Binary-black-hole initial data with nearly extremal spins, Phys. Rev. D 78, 084017 (2008).
[247] P. Marronetti, G.J. Mathews, and J.R. Wilson : Irrotational binary neutron stars in quasiequilibrium, Phys. Rev. D 60, 087301 (1999).
[248] P. Marronetti, W. Tichy, B. Brügmann, J. González, M. Hannam, S. Husa, and U. Sperhake : Binary black holes on a budget: simulations using workstations, Class. Quantum Grav. 24, S43 (2007).
[249] K. Martel and E. Poisson : Regular coordinate systems for Schwarzschild and other spherical spacetimes, Am. J. Phys. 69, 476 (2001).
[250] J. M. Martí, J. M. Ibáñez, and J. A. Miralles : Numerical relativistic hydrodynamics: Local characteristic approach, Phys. Rev. D 43, 3794 (1991).
[251] G.J. Mathews and J.R. Wilson : Revised relativistic hydrodynamical model for neutron-star binaries, Phys. Rev. D 61, 127304 (2000).
[252] K. Matera, T.W. Baumgarte, and E. Gourgoulhon : Shells around black holes: the effect of freely specifiable quantities in Einstein’s constraint equations, Phys. Rev. D 77, 024049 (2008).
[253] D. Maxwell : Solutions of the Einstein Constraint Equations with Apparent Horizon Boundaries, Commun. Math. Phys. 253, 561 (2004).
[254] D. Maxwell : Initial Data for Black Holes and Rough Spacetimes, PhD Thesis, University of Washington (2004).
[255] J. W. Milnor : On manifolds homeomorphic to the 7-sphere, Ann. Math. 64, 399 (1956).
[256] C.W. Misner, K.S. Thorne, and J.A. Wheeler : Gravitation, Freeman, New York (1973).
[257] B.C. Mundim, B.J. Kelly, Y. Zlochower, H. Nakano, and M. Campanelli : Hybrid black-hole binary initial data, Class. Quantum Grav. 28, 134003 (2011).
[258] G. Nagy, O.E. Ortiz, and O.A Reula : Strongly hyperbolic second order Einstein’s evolution equations, Phys. Rev. D 70, 044012 (2004).
[259] T. Nakamura : General Relativistic Colaapse of Axially Symmetric Stars Leading to the Formation of Rotating Black Holes, Prog. Theor. Phys. 65, 1876 (1981).
[260] T. Nakamura : 3D Numerical Relativity, in Relativistic Cosmology, Proceedings of the 8th Nishinomiya-Yukawa Memorial Symposium, edited by M. Sasaki, Universal Academy Press, Tokyo (1994), p. 155.
[261] T. Nakamura, K. Oohara, and Y. Kojima : General relativistic collapse to black holes and gravitational waves from black holes, Prog. Theor. Phys. Suppl. 90, 1 (1987).
[262] T. Nakamura and H. Sato : General Relativistic Colaapse of Rotating Supermassive Stars, Prog. Theor. Phys. 66, 2038 (1981).
[263] S. Nissanke : Post-Newtonian freely specifiable initial data for binary black holes in numerical relativity, Phys. Rev. D 73, 124002 (2006).
[264] N. Ó Murchadha and J.W. York : Initial-value problem of general relativity. I. General formulation and physical interpretation, Phys. Rev. D 10, 428 (1974).
[265] R. Oechslin, H.-T. Janka and A. Marek : Relativistic neutron star merger simulations with non-zero temperature equations of state I. Variation of binary parameters and equation of state, Astron. Astrophys. 467, 395 (2007).
[266] R. Oechslin, K. Uryu, G. Poghosyan, and F. K. Thielemann : The Influence of Quark Matter at High Densities on Binary Neutron Star Mergers, Mon. Not. Roy. Astron. Soc. 349, 1469 (2004).
[267] K. Oohara, T. Nakamura, and M. Shibata : A Way to 3D Numerical Relativity, Prog. Theor. Phys. Suppl. 128, 183 (1997).
[268] L.I. Petrich, S.L Shapiro and S.A. Teukolsky : Oppenheimer-Snyder collapse with maximal time slicing and isotropic coordinates, Phys. Rev. D 31, 2459 (1985).
[269] H.P. Pfeiffer : The initial value problem in numerical relativity, in Proceedings Miami Waves Conference 2004 [preprint gr-qc/0412002].
[270] H.P. Pfeiffer, D.A Brown, L.E. Kidder, L. Lindblom, G. Lovelace, and M.A. Scheel : Reducing orbital eccentricity in binary black hole simulations, Class. Quantum Grav. 24, S59 (2007).
[271] H.P. Pfeiffer and J.W. York : Extrinsic curvature and the Einstein constraints, Phys. Rev. D 67, 044022 (2003).
[272] H.P. Pfeiffer and J.W. York : Uniqueness and Nonuniqueness in the Einstein Constraints, Phys. Rev. Lett. 95, 091101 (2005).
[273] T. Piran : Methods of Numerical Relativity, in Rayonnement gravitationnel / Gravitation Radiation, edited by N. Deruelle and T. Piran, North Holland, Amsterdam (1983), p. 203.
[274] E. Poisson : A Relativist’s Toolkit, The Mathematics of Black-Hole
Mechanics, Cambridge Univ. Press, Cambridge (2004);
https://www.physics.uoguelph.ca/poisson/toolkit/
[275] F. Pretorius : Numerical relativity using a generalized harmonic decomposition, Class. Quantum Grav. 22, 425 (2005).
[276] F. Pretorius : Evolution of Binary Black-Hole Spacetimes, Phys. Rev. Lett. 95, 121101 (2005).
[277] F. Pretorius : Simulation of binary black hole spacetimes with a harmonic evolution scheme, Class. Quantum Grav. 23, S529 (2006).
[278] F. Pretorius : Binary Black Hole Coalescence, in Physics of Relativistic Objects in Compact Binaries: From Birth to Coalescence, edited by M. Colpi, P. Casella, V. Gorini, U. Moschella and A. Possenti, Springer, Dordrecht / Canopus, Bristol (2009), p. 305.
[279] T. Regge and C. Teitelboim : Role of surface integrals in the Hamiltonian formulation of general relativity, Ann. Phys. (N.Y.) 88, 286 (1974).
[280] B. Reimann and B. Brügmann : Maximal slicing for puncture evolutions of Schwarzschild and Reissner-Nordström black holes, Phys. Rev. D 69, 044006 (2004).
[281] B.L. Reinhart : Maximal foliations of extended Schwarzschild space, J. Math. Phys. 14, 719 (1973).
[282] A.D. Rendall : Theorems on Existence and Global Dynamics for the
Einstein Equations, Living Rev. Relativity 8, 6 (2005);
https://www.livingreviews.org/lrr-2005-6
[283] O.A. Reula : Hyperbolic Methods for Einstein’s Equations, Living
Rev. Relativity 1, 3 (1998);
https://www.livingreviews.org/lrr-1998-3
[284] O. Reula : Strong Hyperbolicity, lecture at the VII Mexican School on Gravitation and Mathematical Physics (Playa del Carmen, November 26 - December 2, 2006, Mexico); available at https://www.smf.mx/~dgfm-smf/EscuelaVII
[285] O. Rinne : Constrained evolution in axisymmetry and the gravitational collapse of prolate Brill waves, Class. Quantum Grav. 25, 135009 (2008).
[286] M. Saijo : The Collapse of Differentially Rotating Supermassive Stars: Conformally Flat Simulations, Astrophys. J. 615, 866 (2004).
[287] M. Saijo : Dynamical bar instability in a relativistic rotational core collapse, Phys. Rev. D 71, 104038 (2005).
[288] M. Salgado : General relativistic hydrodynamics: a new approach, Rev. Mex. Fís. 44, 0001 (1998).
[289] O. Sarbach and M. Tiglio : Boundary conditions for Einstein’s field equations: mathematical and numerical analysis, J. Hyper. Diff. Equat. 2, 839 (2005).
[290] G. Schäfer : Equations of Motion in the ADM Formalism, lectures at Institut Henri Poincaré, Paris (2006), https://www.luth.obspm.fr/IHP06/
[291] M.A. Scheel, M. Boyle, T. Chu, L.E. Kidder, K.D. Matthews, and H.P. Pfeiffer : High-accuracy waveforms for binary black hole inspiral, merger, and ringdown, Phys. Rev. D 79, 024003 (2009).
[292] M.A. Scheel, H.P. Pfeiffer, L. Lindblom, L.E. Kidder, O. Rinne, and S.A. Teukolsky : Solving Einstein’s equations with dual coordinate frames, Phys. Rev. D 74, 104006 (2006).
[293] R. Schoen and S.-T. Yau : Proof of the Positive Mass Theorem. II., Commun. Math. Phys. 79, 231 (1981).
[294] Y. Sekiguchi, K. Kiuchi, K. Kyutoku, and M. Shibata : Gravitational waves and neutrino emission from the merger of binary neutron stars, Phys. Rev. Lett. 107, 051102 (2011).
[295] Y. Sekiguchi and M. Shibata : Axisymmetric collapse simulations of rotating massive stellar cores in full general relativity: Numerical study for prompt black hole formation, Phys. Rev. D 71, 084013 (2005).
[296] Y. Sekiguchi and M. Shibata : Formation of black hole and accretion disk in a massive high-entropy stellar core collapse, Astrophys. J. 737, 6 (2011).
[297] S.L. Shapiro and S.A. Teukolsky : Collisions of relativistic clusters and the formation of black holes, Phys. Rev. D 45, 2739 (1992).
[298] M. Shibata : Relativistic formalism for computation of irrotational binary stars in quasiequilibrium states, Phys. Rev. D 58, 024012 (1998).
[299] M. Shibata : 3D Numerical Simulations of Black Hole Formation Using Collisionless Particles, Prog. Theor. Phys. 101, 251 (1999).
[300] M. Shibata : Fully General Relativistic Simulation of Merging Binary Clusters — Spatial Gauge Condition, Prog. Theor. Phys. 101, 1199 (1999).
[301] M. Shibata : Fully general relativistic simulation of coalescing binary neutron stars: Preparatory tests, Phys. Rev. D 60, 104052 (1999).
[302] M. Shibata : Axisymmetric general relativistic hydrodynamics: Long-term evolution of neutron stars and stellar collapse to neutron stars and black holes, Phys. Rev. D 67, 024033 (2003).
[303] M. Shibata : Collapse of Rotating Supramassive Neutron Stars to Black Holes: Fully General Relativistic Simulations, Astrophys. J. 595, 992 (2003).
[304] M. Shibata, T.W. Baumgarte, and S.L. Shapiro : Stability and collapse of rapidly rotating, supramassive neutron stars: 3D simulations in general relativity, Phys. Rev. D 61, 044012 (2000).
[305] M. Shibata, T.W. Baumgarte, and S.L. Shapiro : The Bar-Mode Instability in Differentially Rotating Neutron Stars: Simulations in Full General Relativity, Astrophys. J. 542, 453 (2000).
[306] M. Shibata, Y.T. Liu, S.L. Shapiro, and B.C. Stephens : Magnetorotational collapse of massive stellar cores to neutron stars: Simulations in full general relativity, Phys. Rev. D 74, 104026 (2006).
[307] M. Shibata and T. Nakamura : Conformal Time Slicing Condition in Three Dimensional Numerical Relativity, Prog. Theor. Phys. 88, 317 (1992).
[308] M. Shibata and T. Nakamura : Evolution of three-dimensional gravitational waves: Harmonic slicing case, Phys. Rev. D 52, 5428 (1995).
[309] M. Shibata and Y. Sekiguchi : Three-dimensional simulations of stellar core collapse in full general relativity: Nonaxisymmetric dynamical instabilities, Phys. Rev. D 71, 024014 (2005).
[310] M. Shibata and Y. Sekiguchi : Magnetohydrodynamics in full general relativity: Formulation and tests, Phys. Rev. D 72, 044014 (2005).
[311] M. Shibata and K. Taniguchi : Merger of binary neutron stars to a black hole: Disk mass, short gamma-ray bursts, and quasinormal mode ringing, Phys. Rev. D 73, 064027 (2006).
[312] M. Shibata, K. Taniguchi, and K. Uryu : Merger of binary neutron stars of unequal mass in full general relativity, Phys. Rev. D 68, 084020 (2003).
[313] M. Shibata, K. Taniguchi, and K. Uryu : Merger of binary neutron stars with realistic equations of state in full general relativity, Phys. Rev. D 71, 084021 (2005).
[314] M. Shibata and K. Uryu : Simulation of merging binary neutron stars in full general relativity: Γ = 2 case, Phys. Rev. D 61, 064001 (2000).
[315] M. Shibata and K. Uryu : Gravitational Waves from the Merger of Binary Neutron Stars in a Fully General Relativistic Simulation, Prog. Theor. Phys. 107, 265 (2002).
[316] M. Shibata and K. Uryu : Merger of black hole-neutron star binaries: Nonspinning black hole case, Phys. Rev. D 74, 121503(R) (2006).
[317] M. Shibata, K. Uryu, and J.L. Friedman : Deriving formulations for numerical computation of binary neutron stars in quasicircular orbits, Phys. Rev. D 70, 044044 (2004); errata in Phys. Rev. D 70, 129901(E) (2004).
[318] H. Shinkai : Introduction to Numerical Relativity, lecture notes for
APCTP Winter School on Gravitation and Cosmology, Jan 17-18 2003
(Seoul, Korea),
available at https://www.einstein1905.info/winterAPCTP/
[319] H. Shinkai and G. Yoneda : Re-formulating the Einstein equations for stable numerical simulations: Formulation Problem in Numerical Relativity, to appear (?) in Progress in Astronomy and Astrophysics (Nova Science Publ.), preprint gr-qc/0209111.
[320] L. Smarr : Gauge conditions, radiation formulae and the two black hole collisions, in Sources of Gravitational Radiation, edited by L.L. Smarr, Cambridge Univ. Press, Cambridge (1979), p. 245.
[321] L. Smarr, A. Čadež, B. DeWitt, and K. Eppley : Collision of two black holes: Theoretical framework, Phys. Rev. D 14, 002443 (1976).
[322] L. Smarr and J.W. York : Radiation gauge in general relativity, Phys. Rev. D 17, 1945 (1978).
[323] L. Smarr and J.W. York : Kinematical conditions in the construction of spacetime, Phys. Rev. D 17, 2529 (1978).
[324] U. Sperhake : Binary black-hole evolutions of excision and puncture data, Phys. Rev. D 76, 104015 (2007).
[325] R.F. Stark and T. Piran : Gravitational-Wave Emission from Rotating Gravitational Collapse, Phys. Rev. Lett. 55, 891 (1985).
[326] J.M. Stewart : The Cauchy problem and the initial boundary value problem in numerical relativity, Class Quantum Grav. 15, 2865 (1998).
[327] N. Straumann : General Relavity, with Applications to Astrophysics, Springer-Verlag, Berlin (2004).
[328] L.B. Szabados : Quasi-Local Energy-Momentum and Angular
Momentum in General Relativity, Living Rev. Relativity 12, 4 (2009)
;
https://www.livingreviews.org/lrr-2009-4
[329] K. Taniguchi, T.W. Baumgarte, J.A. Faber, and S.L. Shapiro : Quasiequilibrium sequences of black-hole-neutron-star binaries in general relativity, Phys. Rev. D 74, 041502(R) (2006).
[330] K. Taniguchi, T.W. Baumgarte, J.A. Faber, and S.L. Shapiro : Quasiequilibrium black hole-neutron star binaries in general relativity, Phys. Rev. D 75, 084005 (2007).
[331] K. Taniguchi, T.W. Baumgarte, J.A. Faber, and S.L. Shapiro : Relativistic black hole-neutron star binaries in quasiequilibrium: Effects of the black hole excision boundary condition, Phys. Rev. D 77, 044003 (2008).
[332] K. Taniguchi and E. Gourgoulhon : Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity. III. Identical and different mass stars with γ = 2, Phys. Rev. D 66, 104019 (2002).
[333] K. Taniguchi and E. Gourgoulhon : Various features of quasiequilibrium sequences of binary neutron stars in general relativity, Phys. Rev. D 68, 124025 (2003).
[334] K. Taniguchi and M. Shibata : Binary neutron stars in quasi-equilibrium, Astrophys. J. Suppl. Ser. 188, 187 (2010).
[335] C. H. Taubes : Gauge theory on asymptotically periodic 4-manifolds, J. Differential Geom. 25, 363 (1987).
[336] S.A. Teukolsky : Linearized quadrupole waves in general relativity and the motion of test particles, Phys. Rev. D 26, 745 (1982).
[337] S.A Teukolsky : Irrotational binary neutron stars in quasi-equilibrium in general relativity, Astrophys. J. 504, 442 (1998).
[338] M. Thierfelder, S. Bernuzzi, and B. Brügmann : Numerical relativity simulations of binary neutron stars, Phys. Rev. D 84, 044012 (2011).
[339] K.S. Thorne and D. Macdonald : Electrodynamics in curved spacetime: 3+1 formulation, Mon. Not. R. Astron. Soc. 198, 339 (1982).
[340] W. Tichy, B. Brügmann, M. Campanelli, and P. Diener : Binary black hole initial data for numerical general relativity based on post-Newtonian data, Phys. Rev. D 67, 064008 (2003).
[341] A.A. Tsokaros and K. Uryu : Numerical method for binary black hole/neutron star initial data: Code test, Phys. Rev. D 75, 044026 (2007).
[342] K. Uryu and Y. Eriguchi : New numerical method for constructing quasiequilibrium sequences of irrotational binary neutron stars in general relativity, Phys. Rev. D 61, 124023 (2000).
[343] K. Uryu, M. Shibata, and Y. Eriguchi : Properties of general relativistic, irrotational binary neutron stars in close quasiequilibrium orbits: Polytropic equations of state, Phys. Rev. D 62, 104015 (2000).
[344] K. Uryu, F. Limousin, J.L. Friedman, E. Gourgoulhon, and M. Shibata : Binary Neutron Stars: Equilibrium Models beyond Spatial Conformal Flatness, Phys. Rev. Lett. 97, 171101 (2006).
[345] K. Uryu, F. Limousin, J. L. Friedman, E. Gourgoulhon, and M. Shibata : Nonconformally flat initial data for binary compact objects, Phys. Rev. D 80, 124004 (2009).
[346] J.A. Valiente Kroon : Nonexistence of Conformally Flat Slices in Kerr and Other Stationary Spacetimes, Phys. Rev. Lett. 92, 041101 (2004).
[347] B. van der Holst, R. Keppens, and Z. Meliani : A multidimensional grid-adaptive relativistic magnetofluid code, Comput. Phys. Com. 179, 617 (2008).
[348] J.R. van Meter, J.G. Baker, M. Koppitz, and D.I. Choi : How to move a black hole without excision: gauge conditions for the numerical evolution of a moving puncture, Phys. Rev. D 73, 124011 (2006).
[349] N. Vasset, J. Novak, and J.L. Jaramillo : Excised black hole spacetimes: Quasilocal horizon formalism applied to the Kerr example, Phys. Rev. D 79, 124010 (2009).
[350] R.M. Wald : General relativity, University of Chicago Press, Chicago (1984).
[351] D. Walsh : Non-uniqueness in conformal formulations of the Einstein Constraints, Class. Quantum Grav. 24, 1911 (2007).
[352] J.A. Wheeler : Geometrodynamics and the issue of the final state, in Relativity, Groups and Topology, edited by C. DeWitt and B.S. DeWitt, Gordon and Breach, New York (1964), p. 316.
[353] J.R. Wilson : Numerical Study of Fluid Flow in a Kerr Space, Astrophys. J. 173, 431 (1972).
[354] J.R. Wilson and G.J. Mathews : Relativistic hydrodynamics, in Frontiers in numerical relativity, edited by C.R. Evans, L.S. Finn and D.W. Hobill, Cambridge Univ. Press, Cambridge (1989), p. 306.
[355] J. Winicour : Characteristic Evolution and Matching, Living Rev.
Relativity 12, 3 (2009);
https://www.livingreviews.org/lrr-2009-3
[356] E. Witten : A New Proof of the Positive Energy Theorem, Commun. Math. Phys. 80, 381 (1981).
[357] T. Yamamoto, M. Shibata, and K. Taniguchi : Simulating coalescing compact binaries by a new code, Phys. Rev. D 78, 064054 (2008).
[358] J.W. York : Gravitational Degrees of Freedom and the Initial-Value Problem, Phys. Rev. Lett. 26, 1656 (1971).
[359] J.W. York : Role of Conformal Three-Geometry in the Dynamics of Gravitation, Phys. Rev. Lett. 28, 1082 (1972).
[360] J.W. York : Mapping onto Solutions of the Gravitational Initial Value Problem, J. Math. Phys. 13, 125 (1972).
[361] J.W. York : Conformally invariant orthogonal decomposition of symmetric tensors on Riemannian manifolds and the initial-value problem of general relativity, J. Math. Phys. 14, 456 (1973).
[362] J.W. York : Covariant decompositions of symmetric tensors in the
theory of gravitation, Ann. Inst. Henri Poincaré A 21, 319 (1974);
available at
https://www.numdam.org/item?id=AIHPA_1974__21_4_319_0
[363] J.W. York : Kinematics and dynamics of general relativity, in Sources of Gravitational Radiation, edited by L.L. Smarr, Cambridge Univ. Press, Cambridge (1979), p. 83.
[364] J.W. York : Energy and Momentum of the Gravitational Field, in Essays in General Relativity, a Festschrift for Abraham Taub, edited by F.J. Tipler, Academic Press, New York (1980), p. 39.
[365] J.W. York : Conformal “thin-sandwich” data for the initial-value problem of general relativity, Phys. Rev. Lett. 82, 1350 (1999).
[366] J.W. York : Velocities and Momenta in an Extended Elliptic Form of the Initial Value Conditions, Nuovo Cim. B119, 823 (2004).